Terzaghi's Principle
Terzaghi's Principle states that when a rock is subjected to a stress, it is opposed by the fluid pressure of pores in the rock.[1]
More specifically, Karl von Terzaghi's Principle, also known as Terzaghi's theory of one-dimensional consolidation, states that all quantifiable changes in stress to a soil [compression, deformation, shear resistance] are a direct result of a change in effective stress. The effective stress 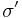 is related to total stress
is related to total stress  and the pore pressure
and the pore pressure  by the relationship;
by the relationship;
reading that total stress is equal to the sum of effective stress and pore water pressure.
Contents |
Assumptions of Terzaghi's Principle
- The soil is homogenous (uniform in composition throughout).
- The soil is fully saturated (zero air voids due to water content being so high).
- The solid particles and water are incompressible.
- Compression and flow are one-dimensional (vertical axis being the one of interest).
- Strains in the soil are relatively small.
- Darcy's Law is valid for all hydraulic gradients.
- The coefficient of permeability and the coefficient of volume compressibility remain constant throughout the process.
- There is a unique relationship, independent of time, between the void ratio and effective stress.
Validity
Though the first 5 assumptions are either likely to hold, or deviation will have no discernible effect, experimental results contradict the final 3. Darcy's Law does not seem to hold at low hydraulic gradients, and both the coefficients of permeability and volume compressibility decrease during consolidation. This is due to the non-linearity of the relationship between void ratio and effective stress, although for small stress increments assumption 7 is reasonable. Finally, the relationship between void ratio and effective stress is not independent on time, again proven by experimental results.
See also
- ^ Laws and models: science, engineering, and technology. C. W. Hall, pp 444. 2000.